在实际生产中,可能会碰到一种比较头疼的问题,那就是分类问题中类别型的因变量可能存在严重的不平衡,即类别之间的比例严重失调。
为了解决数据的非平衡问题,2002年Chawla提出了SMOTE算法,并受到学术界和工业界的一致认同。本文将对SMOTE算法,SMOTE算法的几个变形,以及一个SMOTE算法的主流开源实现的源码进行分析。
1. 数据不均衡问题概述
1.1 常见的数据不平衡场景
医学影像:癌细胞识别,健康细胞和癌细胞的比例20:1
保险:车险报销数据集,报销和未报销比例26:1
天文学:其他记录和太阳风记录,比例26 : 1

CTR:未点击和点击记录比例57:1

除了以上例子以外,数据不平衡问题的场景还有:欺诈性交易,识别客户流失率(其中绝大多数顾客都会继续使用该项服务),自然灾害,例如地震等等。
1.2 不平衡场景下的准确率评估
当面临不平衡的数据集的时候,机器学习算法倾向于产生不太令人满意的分类器。对于任何一个不平衡的数据集,如果要预测的事件属于少数类别,并且事件比例小于 5%,那就通常将其称为罕见事件(rare event)。在不平衡领域时,准确率并不是一个用来衡量模型性能的合适指标。
在一个公用事业欺诈检测数据集中,有以下数据:
总观测 = 1000
欺诈观测(正样本) = 20
非欺诈观测 (负样本)= 980
罕见事件比例 = 2%
在这个例子中,如果一个分类器将所有属于大部分类别的实例都正确分类,实现了 98% 的准确率;而把占 2% 的少数观测数据视为噪声并消除了。但实际上我们真正关心的是被消除的那2%的少数类样本。
所以这种情况下,准确率严重高估了模型的表现。
1.3 不平衡场景下的AUC评估
在评估模型在不平衡数据集上的表现时,应该使用AUC,即ROC曲线的面积。ROC曲线是指一个模型的threshold在连续变换时对应的真正例率和假正例率围成的曲线。
假正例率:FPR = FP/(TN+FP),把一个负样本错当成正样本的概率。
真正例率:TPR= TP/(TP +FN),把一个正样本分对的概率。
当然是FPR越低越好,TPR越高越好。
AUC值是一个概率值,当你随机挑选一个正样本以及负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值,AUC值越大,当前分类算法越有可能将正样本排在负样本前面,从而能够更好地分类。
AUC的一般判断标准:
- 0.1 - 0.5:模型的表现比随机猜测还差
- 0.5 - 0.7:效果较低,但用于预测股票已经很不错了
- 0.7 - 0.85:效果一般
- 0.85 - 0.95:效果很好
- 0.95 - 1:效果非常好,但一般不太可能
下面几个小动画可以帮助大家更好得理解AUC:
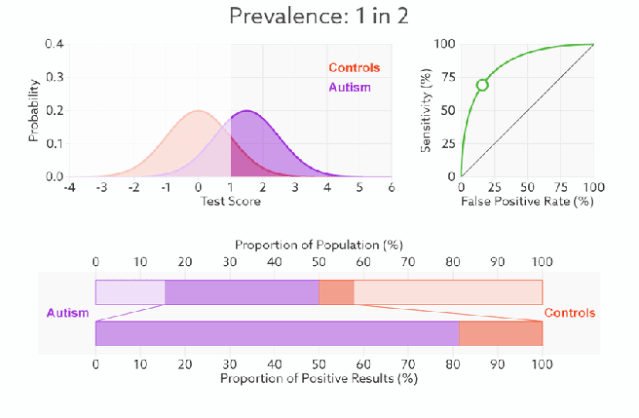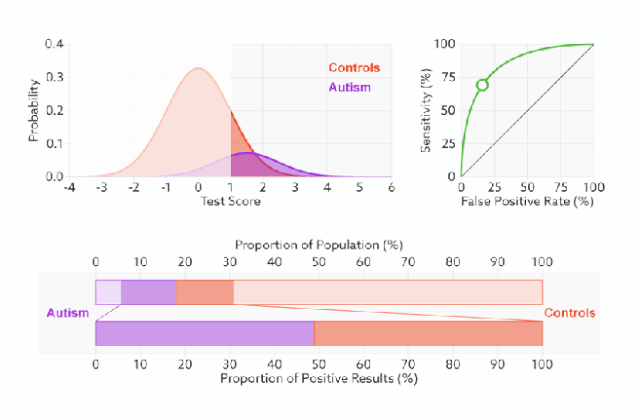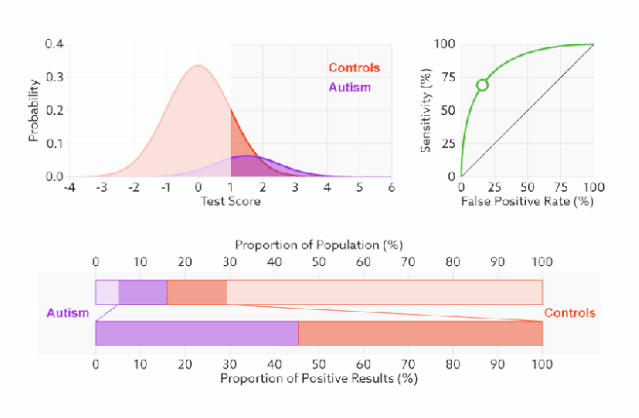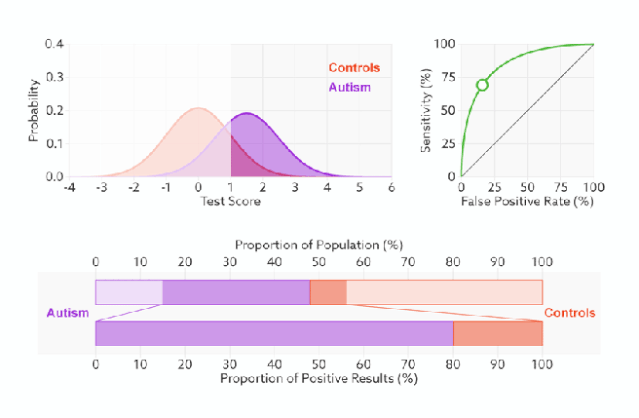
左图中橙色的曲线是指负样本(多数类)的分布,紫色的曲线是指正样本(少数类)的分布,两条曲线中间透明的边界就是模型用于把概率转换为0/1的阈值(e.g,逻辑回归中的默认的0.5),右图就是在正负样本分布以及阈值变化时不同的ROC曲线。
分类器的分类性能越好,即把正负样本分开能力越强时,真正例率越高,假正例率越低,这样ROC曲线就越往左上方偏斜,当ROC曲线为一条45度直线时,表示模型的区分能力等同于随机乱猜。
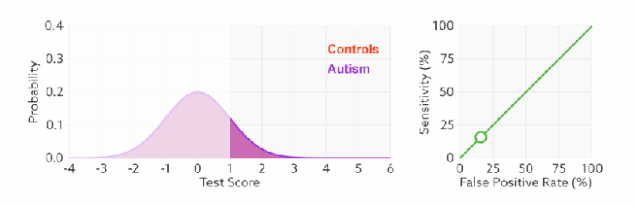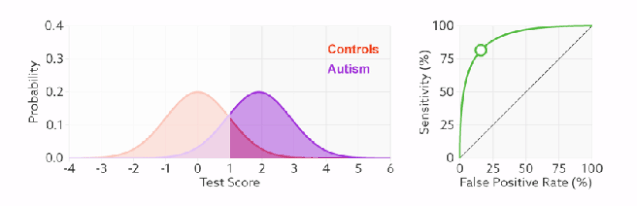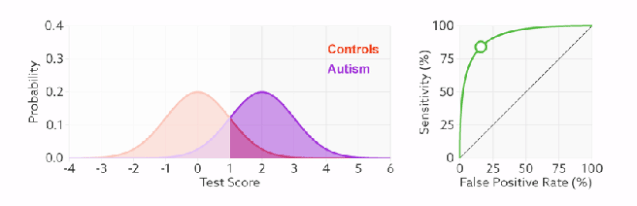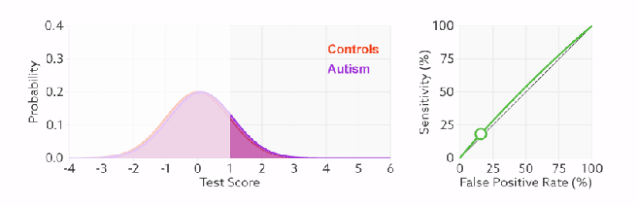
ROC曲线的绘制和PR曲线一样,即遍历模型的所有Threshold,计算当前Threshold下的FTR和PTR,然后把所有Threshlod下的(FPR, TPR)连成一条曲线。可以看出,阈值变化时不会影响模型的AUC值的。
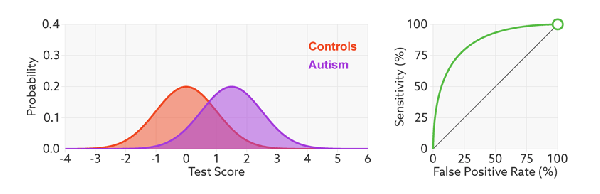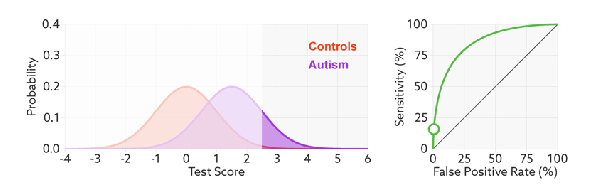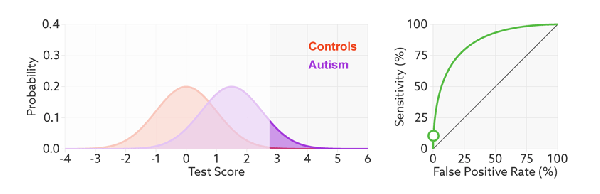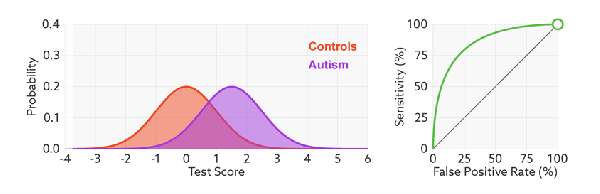
当面临不平衡的数据集的时候,ROC曲线无视样本不均衡的情况,只考虑模型的分类能力,如图,正负样本的比例变化时,模型的区分能力不变,ROC曲线的形状是不会变的。所以对模型在不平衡数据集上的性能评估最好使用AUC而不是Accuray。
1.4 小实验:不平衡数据对模型表现的影响
这里用一个小实验测试模型在正负样本不同比例下的表现。
sklearn.datasets make_classification
from sklearn.datasets import *from sklearn.model_selection import *from sklearn import treefrom sklearn.metrics import *import pandas as pdimport numpy as npimport matplotlib.pyplot as plt#决策边界绘制函数def plot_decision_boundary(X_in,y_in,pred_func): x_min, x_max = X_in[:, 0].min() - .5, X_in[:, 0].max() + .5 y_min, y_max = X_in[:, 1].min() - .5, X_in[:, 1].max() + .5 h = 0.01 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = pred_func(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.contourf(xx, yy, Z,cmap=plt.get_cmap('GnBu')) plt.scatter(X_in[:, 0], X_in[:, 1], c=y_in,cmap=plt.get_cmap('GnBu'))#在不同的正负样本比例下训练决策树,并画出决策边界,计算AUCfor weight_minority in [0.01,0.05,0.1,0.2,0.5]:X,y=make_classification(n_samples=500,n_features=2,n_redundant=0,random_state=2,n_clusters_per_class=1,weights=(weight_minority,1-weight_minority)) plt.scatter(X[:,0],X[:,1],c=y) X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,random_state=6) clf = tree.DecisionTreeClassifier() clf = clf.fit(X_train, y_train) plot_decision_boundary(X,y,lambda x: clf.predict(x)) plt.ion() plt.title("Decision Tree with imbalance rate: "+str(weight_minority)) plt.show() print("current auc:"+str(roc_auc_score(y_test, clf.predict(X_test)))) print("----------------------------------")
(左右滑动查看完整代码,下同)
正负样本比例1:100,AUC:0.5

正负样本比例1:20,AUC:0.8039
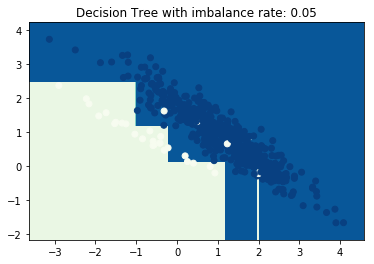
正负样本比例1:10,AUC:0.9462
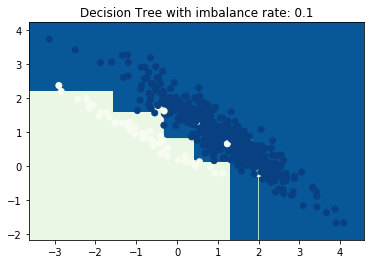
正负样本比例1:5,AUC:0.9615
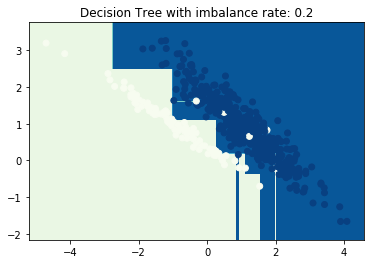
正负样本比例1:1,AUC:0.9598

可见在样本不平衡的时候,模型的表现较差,当少数类的比例升高后,模型的auc迅速提升,分离边界也更加合理,在比例继续升高的时候auc有少许下降是因为正负样本发生了重叠。
2. 应对数据不均衡问题的常用方法
这一节会对常用的应对数据不均衡的方法进行一个简单的总结,按照样本处理方式可以分为4类:过采样,欠采样,过采样+欠采样以及异常检测。
2.1 过采样
随机过采样:随机抽取负样本复制多份。
Smote:采用插值方法生成新样本,具体原理会在第三节详述。
Adasyn:原理与Smote类似,只是选取种子样本时会用一个KNN分类器选择那些更加容易分错的样本。
2.2 欠采样
随机欠采样
随机从多数类样本中抽取一部分数据进行删除,随机欠采样有一个很大的缺点是未考虑样本的分布情况,而采样过程又具有很大的随机性,可能会误删多数类样本中一些重要的信息。
EasyEnsemble
将多数类样本随机划分成n个子集,每个子集的数量等于少数类样本的数量,这相当于欠采样。接着将每个子集与少数类样本结合起来分别训练一个模型,最后将n个模型集成,这样虽然每个子集的样本少于总体样本,但集成后总信息量并不减少。
BalanceCascade
采用了有监督结合Boosting的方式。在第n轮训练中,将从多数类样本中抽样得来的子集与少数类样本结合起来训练一个基学习器H,训练完后多数类中能被H正确分类的样本会被剔除。
在接下来的第n+1轮中,从被剔除后的多数类样本中产生子集用于与少数类样本结合起来训练,最后将不同的基学习器集成起来。BalanceCascade的有监督表现在每一轮的基学习器起到了在多数类中选择样本的作用,而其Boosting特点则体现在每一轮丢弃被正确分类的样本,进而后续基学习器会更注重那些之前分类错误的样本。
NearMiss
一种原型选择(prototype selection)方法,即从多数类样本中选取最具代表性的样本用于训练,主要是为了缓解随机欠采样中的信息丢失问题。NearMiss采用一些启发式的规则来选择样本,根据规则的不同可分为3类:
- NearMiss-1:选择到最近的K个少数类样本平均距离最近的多数类样本。 NearMiss-2:选择到最远的K个少数类样本平均距离最近的多数类样本。 NearMiss-3:对于每个少数类样本选择K个最近的多数类样本,目的是保证每个少数类样本都被多数类样本包围。
Tomek Link
Tomek Link表示不同类别之间距离最近的一对样本,即这两个样本互为最近邻且分属不同类别。这样如果两个样本形成了一个Tomek Link,则要么其中一个是噪音,要么两个样本都在边界附近。这样通过移除Tomek Link就能“清洗掉”类间重叠样本,使得互为最近邻的样本皆属于同一类别,从而能更好地进行分类。
Edited Nearest Neighbours (ENN)
对于属于多数类的一个样本,如果其K个近邻点有超过一半都不属于多数类,则这个样本会被剔除。这个方法的另一个变种是所有的K个近邻点都不属于多数类,则这个样本会被剔除。
最后,数据清洗技术最大的缺点是无法控制欠采样的数量。由于都在某种程度上采用了K近邻法,而事实上大部分多数类样本周围也都是多数类,因而能剔除的多数类样本比较有限。
2.3 过采样+欠采样
很多实验表明结合过采样和欠采样比单独使用这两种方法会有更好的效果,常用的过采样和欠采样组合包括SMOTE + ENN、SMOTE + Tomek。
2.4 异常检测方法
当少数类的样本并不属于同一种分布时,可以考虑使用异常检测方法区分多数类和少数类。
统计方法检测
统计方法也比较简单,一般分两步:
- 先假设全量数据服从一定的分布,比如常见的正太分布,泊松分布等;
- 再计算每个点属于这个分布的概率,也就是常见的以平均值和方差确定密度函数的问题。
OneClassSVM
只有一类的信息是可以用于训练,其他类别的(总称outlier)信息是缺失的,也就是区分两个类别的边界线是通过仅有的一类数据的信息学习得到的。寻找一个超平面将样本中的正例圈出来,预测就是用这个超平面做决策,在圈内的样本就认为是正样本。
孤立森林
在孤立森林(iForest)中,异常被定义为“容易被孤立的离群点 (more likely to be separated)”,可以将其理解为分布稀疏且离密度高的群体较远的点。在特征空间里,分布稀疏的区域表示事件发生在该区域的概率很低,因而可以认为落在这些区域里的数据是异常的。
孤立森林是一种适用于连续数据(Continuous numerical data)的无监督异常检测方法,即不需要有标记的样本来训练,但特征需要是连续的。对于如何查找哪些点容易被孤立(isolated),iForest使用了一套非常高效的策略。在孤立森林中,递归地随机分割数据集,直到所有的样本点都是孤立的。在这种随机分割的策略下,异常点通常具有较短的路径。
3. Smote算法及其变形的原理
3.1 什么是SMOTE
2002年Chawla提出了SMOTE (synthetic minority oversampling technique) 算法,并受到学术界和工业界的一致认同,SMOTE 的思想概括起来就是在少数类样本之间进行插值来产生额外的样本。
为什么要用SMOTE,直接随机过采样不行吗?下面这个例子来自于SMOTE原始论文。
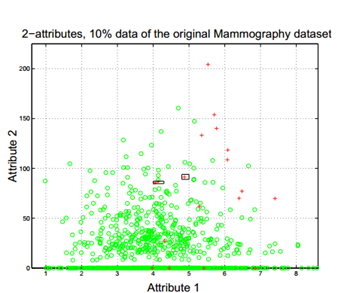
数据取自一个乳腺癌X光片数据集,红色为少数样本,绿色为多数样本,上图为直接随机过采样后训练的决策树分离边界,可见随机过采样存在严重过拟合。模型只学习到了随机过采样的那几个种子样本,而把其他少数类样本都当成了噪声!
具体地,对于一个少数类样本 使用K近邻法(k值需要提前指定),求出离 距离最近的k个少数类样本,其中距离定义为样本之间n维特征空间的欧氏距离。然后从k个近邻点中随机选取一个,使用下列公式生成新样本:
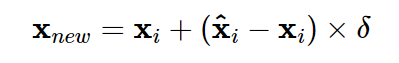
其中 为选出的k近邻点,δ∈[0,1]是一个随机数。下图就是一个SMOTE生成样本的例子,使用的是3-近邻,可以看出SMOTE生成的样本一般就在 和 相连的直线上:
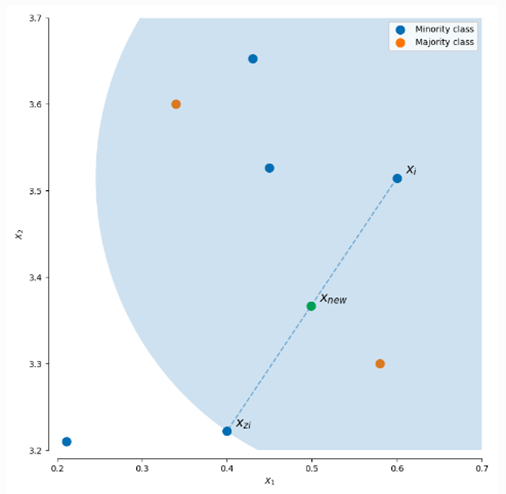
下面是原始论文中的伪代码,感兴趣的同学可以仔细研究一下,其实其中的核心代码就是第22行:插值生成的逻辑。


3.2 Smote算法的变形
Border-line SMOTE
SMOTE会随机选取少数类样本用以合成新样本,而不考虑周边样本的情况,这样容易带来两个问题:
- 如果选取的少数类样本周围也都是少数类样本,则新合成的样本不会提供太多有用信息。这就像支持向量机中远离margin的点对决策边界影响不大。
- 如果选取的少数类样本周围都是多数类样本,这类的样本可能是噪音,则新合成的样本会与周围的多数类样本产生大部分重叠,致使分类困难。
总的来说我们希望新合成的少数类样本能处于两个类别的边界附近,这样往往能提供足够的信息用以分类。而这就是下面的 Border-line SMOTE 算法要做的事情。
这个算法会先将所有的少数类样本分成三类,如下图所示:
- "noise" :所有的k近邻个样本都属于多数类
- "danger" :超过一半的k近邻样本属于多数类
- "safe":超过一半的k近邻样本属于少数类
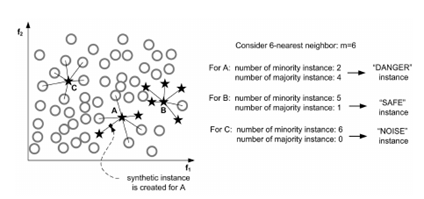
Border-line SMOTE算法只会从处于”danger“状态的样本中随机选择,然后用SMOTE算法产生新的样本。处于”danger“状态的样本代表靠近”边界“附近的少数类样本,而处于边界附近的样本往往更容易被误分类。因而 Border-line SMOTE 只对那些靠近”边界“的少数类样本进行人工合成样本,而 SMOTE 则对所有少数类样本一视同仁。
SVM SMOTE
使用一个SVM分类器寻找支持向量,然后在支持向量的基础上合成新的样本。类似Broderline Smote,SVM smote也会根据K近邻的属性决定样本的类型(safe,danger,noice),然后使用danger的样本训练SVM。
Kmeans SMOTE
在合成样本之前先对样本进行聚类,然后根据簇密度的大小分别对不同簇的负样本进行合成。在聚类步骤中,使用k均值聚类为k个组。过滤选择用于过采样的簇,保留具有高比例的少数类样本的簇。然后,它分配合成样本的数量,将更多样本分配给少数样本稀疏分布的群集。最后,过采样步骤,在每个选定的簇中应用SMOTE以实现少数和多数实例的目标比率。
SMOTE-NC
以上的Smote方法都不能处理分类变量,SMOTE-NC由于分类变量无法计算插值,SMOTE-NC会在合成新样本的时候参考新样本最近邻的该特征,然后区其中出现次数最多的值。
下图是Smote几种变形的过采样结果可视化:
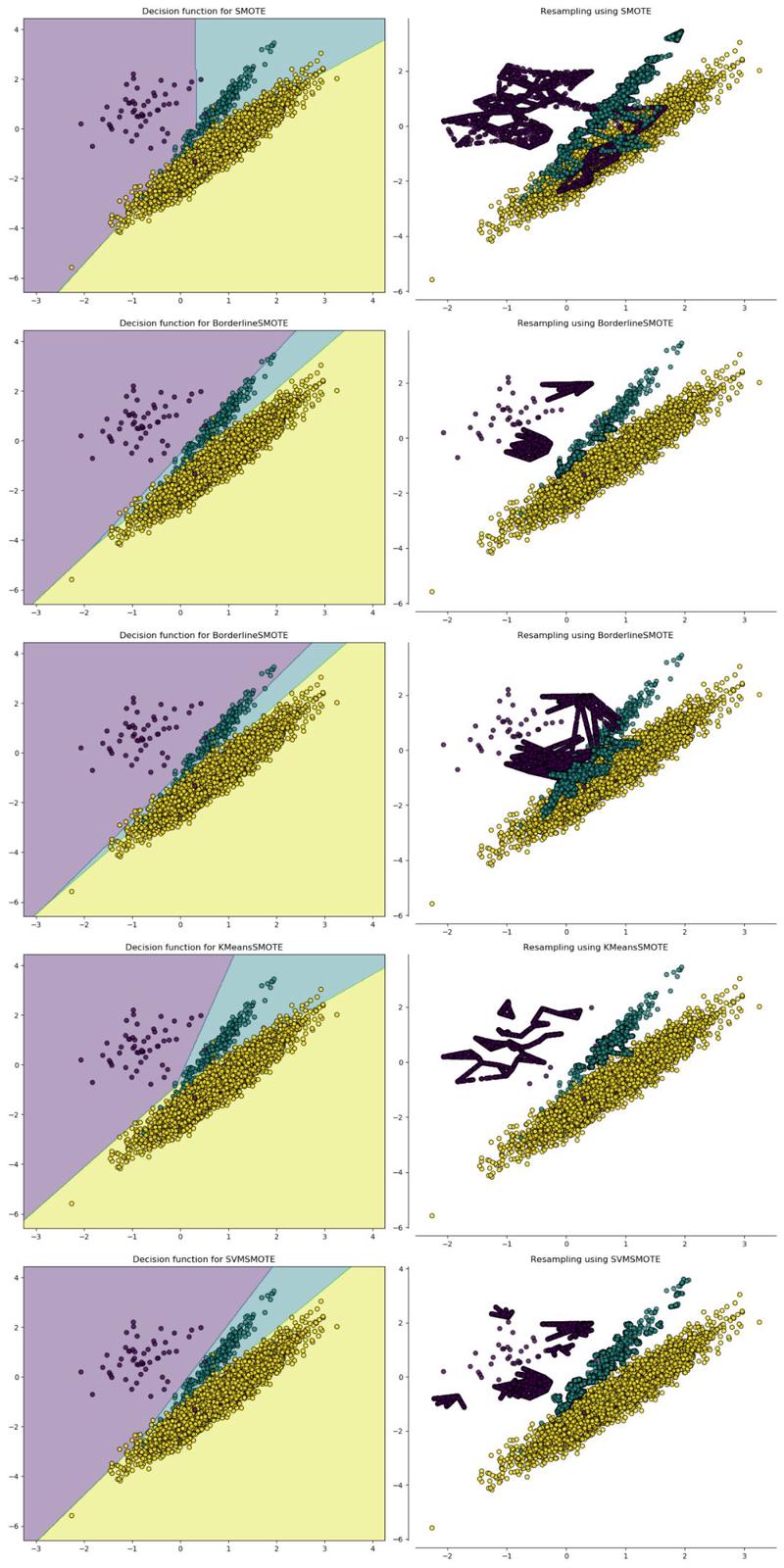
可见使用原始Smote的话,插值产生的新样本很可能会穿过正确的分离边界,进入其他类的区域,而其他变形则很好地解决了这个问题。
4. 开源实现Imbalanced_learn中的smote实现
市面上Smote的一个主流实现是来自于sklearn的contrib项目imbalanced_learn,使用imbalanced_learn的smote符合sklearn的API规范,下面是一段使用smote的示例代码:
>>> from collections import Counter>>> from sklearn.datasets import make_classification>>> from imblearn.over_sampling import SMOTE>>> X, y = make_classification(n_classes=2, class_sep=2,... weights=[0.1, 0.9], n_informative=3, n_redundant=1, flip_y=0,... n_features=20, n_clusters_per_class=1, n_samples=1000, random_state=10)
>>> print('Original dataset shape %s' % Counter(y))Original dataset shape Counter({1: 900, 0: 100})
>>> sm = SMOTE(random_state=42)>>> X_res, y_res = sm.fit_resample(X, y)>>> print('Resampled dataset shape %s' % Counter(y_res))
Resampled dataset shape Counter({0: 900, 1: 900})
源码中的类继承关系如下图:
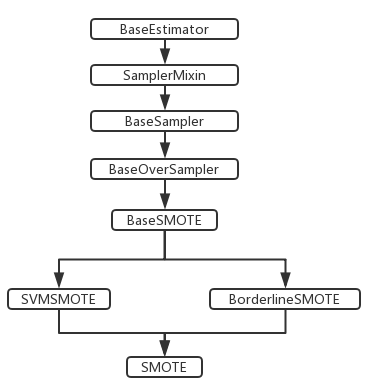
下面我们以boardline_smote为例分析源码,我们将按照从下到上(SMOTE->BorderlineSMOTE->BaseSMOTE)的顺序对几个核心类的关键代码进行分析。
SMOTE
在使用过程中,最基础的类就是SMOTE,SMOTE类即可以使用原始的SMOTE算法,也可以通过传参使用BoardlineSmote和SVMSmote。
fit_resamplefit_resample
_sample
_sample_sample_make_samples_make_samples_make_samples
_sample
class SMOTE(SVMSMOTE, BorderlineSMOTE):
def __init__(self, sampling_strategy='auto', random_state=None, k_neighbors=5, m_neighbors='deprecated', out_step='deprecated', kind='deprecated', svm_estimator='deprecated', n_jobs=1, ratio=None): # FIXME: in 0.6 call super() BaseSMOTE.__init__(self, sampling_strategy=sampling_strategy, random_state=random_state, k_neighbors=k_neighbors, n_jobs=n_jobs, ratio=ratio) self.kind = kind self.m_neighbors = m_neighbors self.out_step = out_step self.svm_estimator = svm_estimator self.n_jobs = n_jobs
#主要用于检测KNN模型实例是否被串用,还有检测当前的Smote实例的类型 def _validate_estimator(self): # FIXME: in 0.6 call super() BaseSMOTE._validate_estimator(self) # FIXME: remove in 0.6 after deprecation cycle
#判断模型类型,把具体类型模型的sample方法绑定到当前对象上 if self.kind != 'deprecated' and not (self.kind == 'borderline-1' or self.kind == 'borderline-2'): if self.kind not in SMOTE_KIND: raise ValueError('Unknown kind for SMOTE algorithm.' ' Choices are {}. Got {} instead.'.format( SMOTE_KIND, self.kind)) else: warnings.warn('"kind" is deprecated in 0.4 and will be ' 'removed in 0.6. Use SMOTE, BorderlineSMOTE or ' 'SVMSMOTE instead.', DeprecationWarning) #以BorderLine为例:如果类型是borderline的话,就是用BorderlineSMOTE类的sample方法 if self.kind == 'borderline1' or self.kind == 'borderline2': self._sample = types.MethodType(BorderlineSMOTE._sample, self) self.kind = ('borderline-1' if self.kind == 'borderline1' else 'borderline-2')
elif self.kind == 'svm': self._sample = types.MethodType(SVMSMOTE._sample, self)
if self.out_step == 'deprecated': self.out_step = 0.5 else: warnings.warn('"out_step" is deprecated in 0.4 and will ' 'be removed in 0.6. Use SVMSMOTE class ' 'instead.', DeprecationWarning)
if self.svm_estimator == 'deprecated': warnings.warn('"svm_estimator" is deprecated in 0.4 and ' 'will be removed in 0.6. Use SVMSMOTE class ' 'instead.', DeprecationWarning) if (self.svm_estimator is None or self.svm_estimator == 'deprecated'): self.svm_estimator_ = SVC(gamma='scale', random_state=self.random_state) elif isinstance(self.svm_estimator, SVC): self.svm_estimator_ = clone(self.svm_estimator) else: raise_isinstance_error('svm_estimator', [SVC], self.svm_estimator)
if self.kind != 'regular': if self.m_neighbors == 'deprecated': self.m_neighbors = 10 else: warnings.warn('"m_neighbors" is deprecated in 0.4 and ' 'will be removed in 0.6. Use SVMSMOTE class ' 'or BorderlineSMOTE instead.', DeprecationWarning)
self.nn_m_ = check_neighbors_object( 'm_neighbors', self.m_neighbors, additional_neighbor=1) self.nn_m_.set_params(**{'n_jobs': self.n_jobs})
# FIXME: to be removed in 0.6 def _fit_resample(self, X, y): self._validate_estimator() return self._sample(X, y)
#采样关键函数 def _sample(self, X, y): # FIXME: uncomment in version 0.6 # self._validate_estimator() X_resampled = X.copy() y_resampled = y.copy()
for class_sample, n_samples in self.sampling_strategy_.items(): if n_samples == 0: continue target_class_indices = np.flatnonzero(y == class_sample) X_class = safe_indexing(X, target_class_indices) # 训练一个KNN分类器得到少数类的K近邻 self.nn_k_.fit(X_class) nns = self.nn_k_.kneighbors(X_class, return_distance=False)[:, 1:] # 真正进行过采样的方法_make_samples,由BaseSMOTE实现 X_new, y_new = self._make_samples(X_class, y.dtype, class_sample, X_class, nns, n_samples, 1.0) # 支持对稠密数据和稀疏数据的过采样 if sparse.issparse(X_new): X_resampled = sparse.vstack([X_resampled, X_new]) sparse_func = 'tocsc' if X.format == 'csc' else 'tocsr' X_resampled = getattr(X_resampled, sparse_func)() else: X_resampled = np.vstack((X_resampled, X_new)) y_resampled = np.hstack((y_resampled, y_new))
return X_resampled, y_resampled
_sample_sample
第一件事和SMOTE中的类似,检查KNN分类器是否被串用,还有就是检查用户使用的是borderline-1还是borderline-2算法。
_make_samples
详细逻辑见代码中的注释。
class BorderlineSMOTE(BaseSMOTE): def __init__(self, sampling_strategy='auto', random_state=None, k_neighbors=5, n_jobs=1, m_neighbors=10, kind='borderline-1'): super().__init__( sampling_strategy=sampling_strategy, random_state=random_state, k_neighbors=k_neighbors, n_jobs=n_jobs, ratio=None) self.m_neighbors = m_neighbors self.kind = kind
def _validate_estimator(self): super()._validate_estimator() self.nn_m_ = check_neighbors_object( 'm_neighbors', self.m_neighbors, additional_neighbor=1) self.nn_m_.set_params(**{'n_jobs': self.n_jobs}) if self.kind not in ('borderline-1', 'borderline-2'): raise ValueError('The possible "kind" of algorithm are ' '"borderline-1" and "borderline-2".' 'Got {} instead.'.format(self.kind))
# FIXME: rename _sample -> _fit_resample in 0.6 def _fit_resample(self, X, y): return self._sample(X, y)
def _sample(self, X, y): self._validate_estimator() #拿到copy X_resampled = X.copy() y_resampled = y.copy()
for class_sample, n_samples in self.sampling_strategy_.items(): if n_samples == 0: continue
#得到少数类的索引 target_class_indices = np.flatnonzero(y == class_sample)
#得到少数类样本列表 X_class = safe_indexing(X, target_class_indices)
#使用全量样本训练KNN模型(这个模型是用来计算危险样本的) self.nn_m_.fit(X)
#得到危险样本的索引列表 danger_index = self._in_danger_noise( self.nn_m_, X_class, class_sample, y, kind='danger')
#如果没有危险样本就跳过 if not any(danger_index): continue
#使用少数类训练一个KNN模型 self.nn_k_.fit(X_class)
#得到危险样本的近邻 nns = self.nn_k_.kneighbors(safe_indexing(X_class, danger_index), return_distance=False)[:, 1:]
# divergence between borderline-1 and borderline-2 #borderline-1 采样做插值的近邻只属于少数类 if self.kind == 'borderline-1': # Create synthetic samples for borderline points. X_new, y_new = self._make_samples( safe_indexing(X_class, danger_index), y.dtype, class_sample, X_class, nns, n_samples) if sparse.issparse(X_new): X_resampled = sparse.vstack([X_resampled, X_new]) else: X_resampled = np.vstack((X_resampled, X_new)) y_resampled = np.hstack((y_resampled, y_new))
#borderline-2 采样做插值的近邻可能属于任何一个类 elif self.kind == 'borderline-2': random_state = check_random_state(self.random_state) fractions = random_state.beta(10, 10)
# only minority X_new_1, y_new_1 = self._make_samples( safe_indexing(X_class, danger_index), y.dtype, class_sample, X_class, nns, int(fractions * (n_samples + 1)), step_size=1.)
# we use a one-vs-rest policy to handle the multiclass in which # new samples will be created considering not only the majority # class but all over classes. X_new_2, y_new_2 = self._make_samples( safe_indexing(X_class, danger_index), y.dtype, class_sample, safe_indexing(X, np.flatnonzero(y != class_sample)), nns, int((1 - fractions) * n_samples), step_size=0.5)
if sparse.issparse(X_resampled): X_resampled = sparse.vstack( [X_resampled, X_new_1, X_new_2]) else: X_resampled = np.vstack((X_resampled, X_new_1, X_new_2)) y_resampled = np.hstack((y_resampled, y_new_1, y_new_2)) return X_resampled, y_resampled
BaseSMOTE
_make_samples_in_danger_noise_generate_sample
_make_samples
_in_danger_noise
_generate_sample
详细代码分析见注释。
SMOTE_KIND = ('regular', 'borderline1', 'borderline2', 'svm')class BaseSMOTE(BaseOverSampler): """Base class for the different SMOTE algorithms.""" def __init__(self, sampling_strategy='auto', random_state=None, k_neighbors=5, n_jobs=1, ratio=None): super().__init__( sampling_strategy=sampling_strategy, ratio=ratio) self.random_state = random_state self.k_neighbors = k_neighbors self.n_jobs = n_jobs
def _validate_estimator(self): """Check the NN estimators shared across the different SMOTE algorithms. """ self.nn_k_ = check_neighbors_object( 'k_neighbors', self.k_neighbors, additional_neighbor=1) self.nn_k_.set_params(**{'n_jobs': self.n_jobs})
#制造合成样本的函数 def _make_samples(self, X, y_dtype, y_type, nn_data, nn_num, n_samples, step_size=1.): """A support function that returns artificial samples constructed along the line connecting nearest neighbours.
Parameters ---------- X : {array-like, sparse matrix}, shape (n_samples, n_features) Points from which the points will be created.
y_dtype : dtype The data type of the targets.
y_type : str or int The minority target value, just so the function can return the target values for the synthetic variables with correct length in a clear format.
nn_data : ndarray, shape (n_samples_all, n_features) Data set carrying all the neighbours to be used
nn_num : ndarray, shape (n_samples_all, k_nearest_neighbours) The nearest neighbours of each sample in `nn_data`.
n_samples : int The number of samples to generate.
step_size : float, optional (default=1.) The step size to create samples.
Returns ------- X_new : {ndarray, sparse matrix}, shape (n_samples_new, n_features) Synthetically generated samples.
y_new : ndarray, shape (n_samples_new,) Target values for synthetic samples.
""" #得到当前的Random_state实例 random_state = check_random_state(self.random_state) #得到一个数组,长度为生成样本数,每个值是生成样本使用的哪个近邻(使用一个数字存储行列坐标,要用的时候在拆出来) samples_indices = random_state.randint( low=0, high=len(nn_num.flatten()), size=n_samples) #步长,默认为1,如果超过一,那生成的样本就是在原始样本和近邻的延长线上 steps = step_size * random_state.uniform(size=n_samples) #除近邻个数得到行数 rows = np.floor_divide(samples_indices, nn_num.shape[1]) #求近邻个数求余得到列数 cols = np.mod(samples_indices, nn_num.shape[1]) #创建生成样本的标签列 y_new = np.array([y_type] * len(samples_indices), dtype=y_dtype)
#如果输入的X是稀疏矩阵 if sparse.issparse(X): #记录行列 row_indices, col_indices, samples = [], [], []
for i, (row, col, step) in enumerate(zip(rows, cols, steps)): #如果当前样本非空 if X[row].nnz: #生成合成样本 sample = self._generate_sample(X, nn_data, nn_num, row, col, step) #记录行列indece row_indices += [i] * len(sample.indices) col_indices += sample.indices.tolist() #记录样本 samples += sample.data.tolist() #返回生成样本构成的稀疏矩阵csr_matrix return (sparse.csr_matrix((samples, (row_indices, col_indices)), [len(samples_indices), X.shape[1]], dtype=X.dtype), y_new)
#如果不是稀疏矩阵 else:#构造返回结果集ndarray X_new = np.zeros((n_samples, X.shape[1]), dtype=X.dtype) for i, (row, col, step) in enumerate(zip(rows, cols, steps)):#对当前的行列生成一个样本,并放到第i个位置 X_new[i] = self._generate_sample(X, nn_data, nn_num, row, col, step) return X_new, y_new‘
#生成样本的函数 def _generate_sample(self, X, nn_data, nn_num, row, col, step): r"""Generate a synthetic sample.
The rule for the generation is:
.. math:: \mathbf{s_{s}} = \mathbf{s_{i}} + \mathcal{u}(0, 1) \times (\mathbf{s_{i}} - \mathbf{s_{nn}}) \,
where \mathbf{s_{s}} is the new synthetic samples, \mathbf{s_{i}} is the current sample, \mathbf{s_{nn}} is a randomly selected neighbors of \mathbf{s_{i}} and \mathcal{u}(0, 1) is a random number between [0, 1).
Parameters ---------- X : {array-like, sparse matrix}, shape (n_samples, n_features) Points from which the points will be created.
nn_data : ndarray, shape (n_samples_all, n_features) Data set carrying all the neighbours to be used.
nn_num : ndarray, shape (n_samples_all, k_nearest_neighbours) The nearest neighbours of each sample in `nn_data`.
row : int Index pointing at feature vector in X which will be used as a base for creating new sample.
col : int Index pointing at which nearest neighbor of base feature vector will be used when creating new sample.
step : float Step size for new sample.
Returns ------- X_new : {ndarray, sparse matrix}, shape (n_features,) Single synthetically generated sample.
""" #X[row]为原始样本 #step是随机比值 #nn_num[row, col]是当前所用的近邻在全量样本中的索引值 #nn_data[nn_num[row, col]]为近邻样本 return X[row] - step * (X[row] - nn_data[nn_num[row, col]])
#检查样本是否处于危险之中或者是噪声 def _in_danger_noise(self, nn_estimator, samples, target_class, y, kind='danger'): """Estimate if a set of sample are in danger or noise.
Used by BorderlineSMOTE and SVMSMOTE.
Parameters ---------- nn_estimator : estimator An estimator that inherits from :class:`sklearn.neighbors.base.KNeighborsMixin` use to determine if a sample is in danger/noise.
samples : {array-like, sparse matrix}, shape (n_samples, n_features) The samples to check if either they are in danger or not.
target_class : int or str The target corresponding class being over-sampled.
y : array-like, shape (n_samples,) The true label in order to check the neighbour labels.
kind : str, optional (default='danger') The type of classification to use. Can be either:
- If 'danger', check if samples are in danger, - If 'noise', check if samples are noise.
Returns ------- output : ndarray, shape (n_samples,) A boolean array where True refer to samples in danger or noise.
""" #拿到目标样本的K近邻放进一个矩阵 x = nn_estimator.kneighbors(samples, return_distance=False)[:, 1:]
#多数类的标签列表,多数类为1,少数类为0 nn_label = (y[x] != target_class).astype(int)
#多数类的个数 n_maj = np.sum(nn_label, axis=1)
#如果是求危险值 if kind == 'danger': # Samples are in danger for m/2 <= m' < m #如果多数类的数量大于大于一半切小于K,那就是危险样本、 #这里使用bitwise对条件值进行按位与,效率比循环高 return np.bitwise_and(n_maj >= (nn_estimator.n_neighbors - 1) / 2, n_maj < nn_estimator.n_neighbors - 1) elif kind == 'noise': # Samples are noise for m = m' #所有的近邻都是多数类,那就是噪声 return n_maj == nn_estimator.n_neighbors - 1 else: raise NotImplementedError
(源码链接:https://github.com/scikit-learn-contrib/imbalanced-learn/tree/master/imblearn/over_sampling)
5. Smote实际应用案例
5.1 Imbalanced_learn中的Smote参数
SMOTE(ratio='auto', random_state-None, k_neighbors=5, m_neighbors=10, out_step=0.5, kind="regular", svm_estimator=None, n_jobs=1)
ratio:用于指定重抽样的比例,如果指定字符型的值,可以是’minority’,表示对少数类别的样本进行抽样、’majority’,表示对多数类别的样本进行抽样、’not minority’表示采用欠采样方法、’all’表示采用过采样方法,默认为’auto’,等同于’all’和’not minority’;如果指定字典型的值,其中键为各个类别标签,值为类别下的样本量;
random_state:用于指定随机数生成器的种子,默认为None,表示使用默认的随机数生成器;
k_neighbors:指定近邻个数,默认为5个;
m_neighbors:指定从近邻样本中随机挑选的样本个数,默认为10个;
kind:用于指定SMOTE算法在生成新样本时所使用的选项,默认为’regular’,表示对少数类别的样本进行随机采样,也可以是’borderline1’、’borderline2’和’svm’;
svm_estimator:用于指定SVM分类器,默认为sklearn.svm.SVC,该参数的目的是利用支持向量机分类器生成支持向量,然后再生成新的少数类别的样本;
n_jobs:用于指定SMOTE算法在过采样时所需的CPU数量,默认为1表示仅使用1个CPU运行算法,即不使用并行运算功能。
5.2 德国电信CHURN用户流失数据集的SMOTE应用
该数据集来源于德国某电信行业的客户历史交易数据,该数据集一共包含条5000记录,17个特征,其中标签churn为二元变量,yes表示客户流失,no表示客户未流失;
剩余的自变量包含客户的是否订购国际长途套餐、语音套餐、短信条数、话费、通话次数等。接下来就利用该数据集,探究非平衡数据转平衡后的效果。
import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom sklearn import model_selectionfrom sklearn import treefrom imblearn.over_sampling import SMOTEfrom sklearn.metrics import *from sklearn.linear_model import LogisticRegression#清洗数据churn=pd.read_csv(r'C:\Users\Administrator\Desktop\Work\data\churn_all.txt',sep='\t')churn=churn.drop(['Instance_ID'],axis=1)col=['State', 'Account Length', 'Area Code', 'Phone', 'Intl Plan', 'VMail Plan', 'VMail Message', 'Day Mins', 'Day Calls', 'Day Charge', 'Eve Mins', 'Eve Calls', 'Eve Charge', 'Night Mins', 'Night Calls', 'Night Charge', 'Intl Mins', 'Intl Calls', 'Intl Charge', 'CustServ Calls', 'churn']churn.columns=colchurn['churn'].value_counts()#正负样本比例5:1plt.rcParams['font.sans-serif']=['Microsoft Yahei']plt.axes(aspect='equal')counts=churn.churn.value_counts()plt.pie(x=counts,labels=pd.Series(counts.index))plt.show()#数据清洗churn.drop(labels=['State','Area Code','Phone'],axis=1,inplace=True)churn['Intl Plan']=churn['Intl Plan'].map({' no':0,' yes':1})churn['VMail Plan']=churn['VMail Plan'].map({' no':0,' yes':1})churn['churn']=churn['churn'].map({' False.':0,' True.':1})#构建训练集和测试集predictors=churn.columns[:-1]X_train,X_test,y_train,y_test=model_selection.train_test_split(churn[predictors],churn.churn,random_state=12)#使用不平衡数据训练lr模型,查看AUClr=LogisticRegression()lr.fit(X_train,y_train)pred=lr.predict(X_test)roc_auc_score(y_test, pred)#打印ROC曲线,计算AUCfpr,tpr,threshold=metrics.roc_curve(y_test,pred)roc_auc=metrics.auc(fpr,tpr)plt.stackplot(fpr,tpr,color='steelblue',alpha=0.5,edgecolor='black')plt.plot(fpr,tpr,color='black',lw=1)plt.plot([0,1],[0,1],color='red',linestyle='--')plt.text(0.5,0.3,'ROC cur (area=%0.3f)' % roc_auc)plt.xlabel('1-Specificity')plt.ylabel('Sensitivity')plt.show()#使用SMOTE进行重采样over_samples=SMOTE(random_state=1234)over_samples_X,over_samples_y=over_samples.fit_sample(X_train,y_train)#采样前后样本数对比print(y_train.value_counts())print(pd.Series(over_samples_y).value_counts())#使用均衡数据训练LR模型lr2=LogisticRegression()lr2.fit(over_samples_X,over_samples_y)fpr,tpr,threshold=metrics.roc_curve(y_test,pred2)roc_auc=metrics.auc(fpr,tpr)plt.stackplot(fpr,tpr,color='steelblue',alpha=0.5,edgecolor='black')plt.plot(fpr,tpr,color='black',lw=1)plt.plot([0,1],[0,1],color='red',linestyle='--')plt.text(0.5,0.3,'ORC cur (area=%0.3f)' % roc_auc)plt.xlabel('1-Specificity')plt.ylabel('Sensitivity')plt.show()
正负样本比例为5:1
欠采样前AUC:0.55
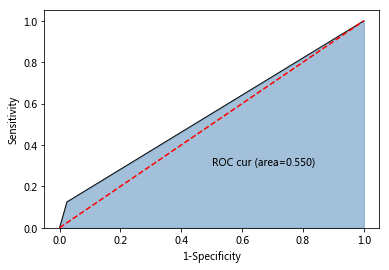
欠采样后AUC:0.735
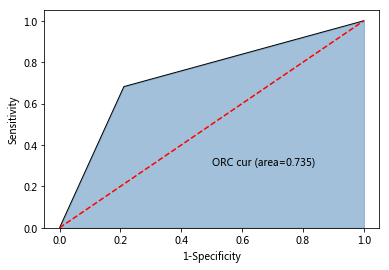
使用过采样数据训练后模型的AUC提升了20%!
参考资料
☆ END ☆



