Sweep Line 算法是由Steve Fortune提出的,这个算法的平均复杂度是O(n),最坏复杂度是O(nlogn)。
设新得到的点集是P = {p1,p2,…,pn};设水平扫描线为L,自上而下,逐点扫描;我们用L+表示L上半平面;用L-表示L的下半平面;用P+表示P中在L上面的点的集合;P-表示P中在L下面的点的集合。P+,P-都是P的子集。如图1所示,当扫描线L在如图位置的时候, L+的局部Voronoi图并不是仅仅由P+构成,而且受P-的影响,所以并不能简单的求出在L+的Voronoi图;但是,我们注意到,L+上的点到L的距离小于到L-上的任意点的距离,从而也就小于P-中的点。那么我们可以把L+这个半平面分成两部分,第一部分称之为A,它们中的每一个点到P+中每个点的距离的最小值小于或等于它们到L的距离;剩余的点构成另外一部分,称之为B。由Voronoi图的定义,我们可以得出,落在A部分的Voronoi图完全由P+上的点决定,因此它们不会随扫描线的下移而改变。那么如何得到A和B的边界呢?我们知道,到一个点和一条直线距离相等的点构成的集合是抛物线,那么,我们如果把所有关于P+上的点和扫描线L的抛物线得到,那么我们依次连接落在最低点的抛物线的曲线,就得到了这个边界(如图2所示),我们称这个边界为波浪线。
那么如何得到Voronoi图的局部呢?在扫描线依次扫描的时候,波浪线随着变化,波浪线只有在扫描线和一个在点集P中的节点相交的时候才会加入新的曲线(如图3所示),在一个新的曲线加入的同时,新的曲线和原来的波浪线的两个交点就在Voronoi图的一条边上,两个交点在扫描线下移的时候沿两个相对的方向扩展,当扫描线到达某个特定位置的时候,其中一个交点就成了Voronoi图的一个顶点,新的Voronoi图的一条边也就完成了,同时波浪线相应的一段曲线也退化成了一个点。我们把扫描线与节点相交的事件称为Site Event,把得到一个Voronoi图的顶点的事件称为Circle Event。一个Site Event在扫描线和节点相交的时候发生,而Circle Event则比较复杂,首先可以证明,当L+中的三个节点共圆,这个圆与L相切,且圆中不包括其它的节点,则这时候Circle Event发生。
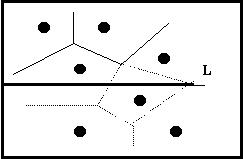
图1 图2
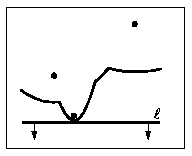
图3
数据结构可以用这样一个树结构来表示各个顶点以及它们的抛物线之间的关系,叶子节点是每个节点,在上一层是相邻的两个节点的抛物线的交点,可以证明这样的交点只有一个。那么增删交点都在这棵结构树来完成。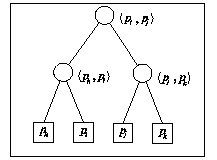
整个算法描述如下:
Algorithm VoronoiDiagram(P)Input: 平面上的节点集。
Output: 用上面所说的树形结构表示的在某个边界的Voronoi图。




