从概率分布的角度考虑,对于一堆样本数据,每个均有特征Xi对应分类标记yi。
生成模型:学习得到联合概率分布P(x,y),即特征x和标记y共同出现的概率,然后求条件概率分布。能够学习到数据生成的机制。
判别模型:学习得到条件概率分布P(y|x),即在特征x出现的情况下标记y出现的概率。
数据要求:生成模型需要的数据量比较大,能够较好地估计概率密度;而判别模型对数据样本量的要求没有那么多。
两者的优缺点如下图,摘自知乎

生成模型:以统计学和Bayes作为理论基础
1、朴素贝叶斯:
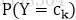

使用极大似然估计(使用样本中的数据分布来拟合数据的实际分布概率)得到先验概率。
2、混合高斯模型:
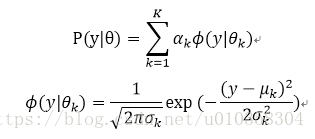
3、隐马尔可夫模型 (HMM)
由隐藏的马尔可夫链随机生成观测序列,是生成模型。HMM是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。包含三要素:初始状态概率向量pie,状态转移概率矩阵A,观测概率矩阵B。
判别模型
1、感知机 (线性分类模型)
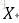
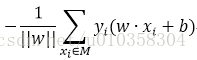
其中M为所有误分类点的集合,||w||可以不考虑。可以使用随机梯度下降得到最后的分类超平面。
2、k近邻法
基于已知样本,对未知样本进行预测时,找到对应的K个最近邻,通过多数表决进行预测。没有显式的学习过程。
3、决策树
决策树在每个单元定义一个类的概率分布,形成一个条件概率分布。决策树中递归地选择最优特征,所谓最优特征即分类效果最好的特征,算法中使用信息增益 (information gain)来衡量,对应公式为:
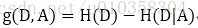
其中D为训练集,A为待测试的特征,H(D)为熵 (经验熵),H(D|A)为条件熵,两者的计算为
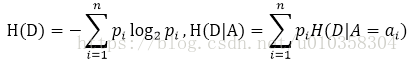
但是以信息增益为划分,存在偏向于选择取值较多的特征,因此使用信息增益比来校正,
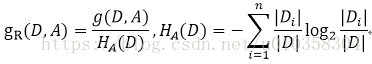
其中n为特征A的取值个数。
4、逻辑斯蒂回归模型
使用条件概率分布表示,
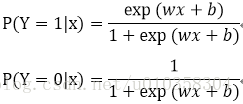
可以使用极大似然估计法估计模型参数,对优化目标使用梯度下降法或者拟牛顿法。
5、最大熵模型
原理:概率模型中,熵最大的模型是最好的模型,可以使用拉格朗日函数求解对偶问题解决。
6、支持向量机 (SVM)
SVM分为线性可分支持向量机 (硬间隔最大化)、线性支持向量机 (软间隔最大化)、非线性支持向量机 (核函数)三种。
目的是最大化间隔,这是和感知机最大的区别。
7、boosting方法 (AdaBoost等)
通过改变训练样本的权重,训练多个分类器,将分类器进行线性组合,提升分类性能。AdaBoost采用加权多数表决的方法。
8、条件随机场 (conditional random field, CRF)
给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。可应用于标注问题。
9、CNN
训练过程中,每一个中间层都有其功能,但其具体的功能无法知道。

